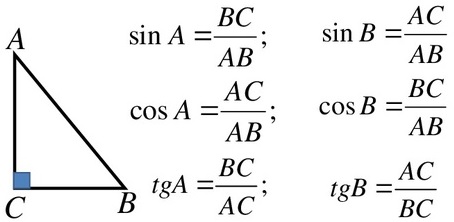Начнём с определений, так как если знаешь, с чем имеешь дело, то проще решать задачи.
Синус:
Синусом острого угла прямоугольного треугольника, называется отношение противолежащего катета к гипотенузе.
Косинус:
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенс:
Тангенсом острого угла прямоугольного треугольника, называется отношение противолежащего катета к прилежащему катету.
У всех этих величин есть значения, которые должны знать:

Их достаточно легко выучить. Мы видим, что sin60 и cos30 равны, аналогично с sin30 и cos60, а значения sin и cos 45 равны вовсе. То есть выучить нам надо только тангенс.
Тангенс можно вычислить если знать синус и косинус данного угла.
Говоря про синусы, косинусы и тангенсы, мы не можем не сказать про основное тригонометрическое тождество:
Помимо формул рассмотренных в статье про площади( http://g99610au.beget.tech/площади-фигур/ ) Для треугольника и ромба есть ещё по формуле для нахождения площадей, связанная с синусами.
Для треугольника:

Для ромба:

Теперь поговорим о их теоремах( а конкретнее синусов и косинусов )
Теорема синусов:
Синусы треугольника пропорциональны синусам противолежащих углов.
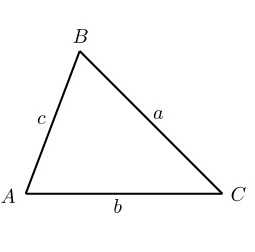
Теорема косинусов(она чем-то напоминает теорему Пифагора):
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон, умноженное на косинус угла между ними.